Two-Sample Z Test in R: Short Guide to Proportions and Means

This blog post will help you learn how to perform a statistical procedure: the two-sample Z test in R. This test is a common hypothesis test used to determine if there is a significant difference between population parameters, typically means or proportions. In a previous post, we covered the basics of the Z test in R. Today, we will focus on how to perform the test.

Two-Sample Z Test for Proportions in R
- Carrying out the Two-Sample Z test
Two Sample Z Test for Means in R
- Carrying out the Z-test
Conclusion
Resources

Two-Sample Z Test for Proportions in R

A two-sample Z test for proportions compares the proportions of success in two independent groups. It is useful when the sample sizes are large enough for the normal approximation to be valid.

Let’s say we conducted two surveys:

In group A, 60 out of 100 people support the new policy.
In group B, 72 out of 120 people support the same policy.

We want to know whether the two groups’ support difference is statistically significant.

Carrying out the Two-Sample Z test

Here is how to carry out a two-sample Z test in R:

# Run two-sample z-test for proportions
prop.test(x, n, correct = FALSE)Code language: PHP (php)

In the code chunk above, we have combined the number of successes and the sample sizes into vectors x and n. Then we used prop.test() with correct = FALSE to run the test for proportions.

Two Sample Z Test for Means in R

We can perform the test for means when comparing the means of two independent groups and assuming known population standard deviations. Although in practice, population standard deviations are often unknown, here’s how the test works with known values:

Let us say:

Group A: mean = 100, standard deviation = 15, sample size = 50
Group B: mean = 105, standard deviation = 15, sample size = 60

We want to know whether the means of two populations are equal.

Carrying out the Z-test

Here is how we can calculate the Z score and the p-value:

# Compute z-score
z <- (mean1 - mean2) / sqrt((sd1^2 / n1) + (sd2^2 / n2))

# Compute p-value (two-tailed)
p_value <- 2 * pnorm(-abs(z))Code language: R (r)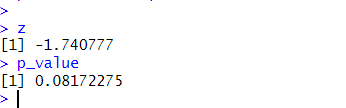

In the code chunk above, we calculated the Z statistic using the means, standard deviations, and sample sizes. Then, we computed the two-tailed p-value to assess significance.

Conclusion

In this post, we learned how to carry out a two-sample Z test in R, specifically for comparing both proportions and means between two independent groups. We used prop.test() for proportions and manually computed the Z statistic for means. If you found this tutorial helpful, please share it on social media and let me know your thoughts in the comments!

Resources

Here are some more data analysis-related tutorials on this page that you might find helpful:

Master MANOVA in R: One-Way, Two-Way, & Interpretation