Multikollinearitet, ett viktigt begrepp inom statistisk analys, syftar på situationen där två eller flera prediktorer i en modell uppvisar hög korrelation. Deta fenomen kan medföra allvarliga implikationer och kan påverka din analys noggrannhet. I kognitionsvetenskap och andra discipliner är förståelsen av problem som detta viktigt, särskilt inom regressionsanalys där det kan snedvrida uppskattningar av prediktorernas individuella effekter. I detta inlägg kommer vi utforska dess definition, betydelse inom statistisk analys, identifiera känsliga analysmetoder, och lära oss hur vi testar och hanterar detta fenomen för att säkerställa korrekta och pålitliga resultat. Ett fokus kommer också att läggas på dess relevans för regressionsanalys och de strategier som kan användas för att mildra dess påverkan.
Table of Contents
- Förkunskaper och Förebredelser
- Vad är Multikollinearitet?
- Varför är det ett problem?
- Vilka analyser påverkas?
- Hur upptäcker man Multikollinearitet?
- Tolkning av Resultaten (Korrelation, VIF, & Tolerans)
- Multikollinearitetstester med Jamovi
- Testning med R
- Vad Gör om Vi har Upptäckt Multikollinearitet ?
- Sammanfattning
- Resurser
Förkunskaper och Förebredelser
För att dra nytta av innehållet i dena bloggpost bör du ha grundläggande kunskaper om regressionsanalys. Det är viktigt att förstå begrepp som prediktorer (oberoende variabler) och beroende variabler, eftersom dessa utgör kärnan i regressionsanalys. Dessutom bör läsarna vara bekanta med sin valda statistikprogramvara, antingen Jamovi eller R, och ha det installerat för att kunna följa steg-för-steg-instruktionerna för multikollinearitetstestning. Om du använder Jamovi, se till att du är bekant med dess gränssnitt och dess funktioner för regressionsanalys. Om du använder R, se till att ha nödvändiga paket installerade (ggplot2 och dplyr) och vara bekväm med att använda dess konsol och skriptsyntax. En grundläggande förståelse för hur man organiserar och förbereder data för regressionsanalys kommer också vara till nytta.
Vad är Multikollinearitet?
Multikollinearitet uppstår när två eller flera prediktorer i en statistisk modell är starkt korrelerade, vilket kan komplicera analysen genom att göra det svårt att särskilja deras individuella effekter. Detta fenomen uttrycks vanligtvis genom höga korrelationskoefficienter mellan prediktorerna, vilket signalerar en överlappande variation i data.
För att belysa detta fenomen kan vi tänka oss en studie inom kognitionsvetenskap där arbetsminne och fluid intelligence används som prediktorer för taligenkänning i brusiga miljöer. Om dessa två prediktorer visar hög korrelation kan det leda till problem och påverka analysens tillförlitlighet.
Ett annat exempel kan hämtas från forskning om självkörande bussar. Om prediktorerna, som kanske inkluderar tekniska specifikationer och vägförhållanden, är starkt korrelerade, kan det påverka förmågan att dra specifika slutsatser om var och en av dessa faktorer.
Varför är det ett problem?
Konsekvenserna av Multikollinearitet:
Multikollinearitet kan ha allvarliga konsekvenser för statistiska analyser, särskilt i regressionsmodeller. Vid tillämpning av metoder som OLS (Ordinary Least Squares) regression för att uppskatta parametrar blir uppskattningarna känsliga för små förändringar i data, vilket ökar standardfel och kan leda till osäkra inferenser. Dessutom kan detta problem förvränga betavärdena, vilket gör det svårt att bedöma den verkliga inverkan av varje prediktor.
Hur det kan påverka tolkningen av resultaten:
När multikollinearitet föreligger blir det utmanande att isolera och mäta den unika effekten av varje prediktor. Tolkningen av resultaten blir tvetydig eftersom hög korrelation mellan prediktorerna gör det svårt att skilja deras individuella bidrag till den beroende variabeln. Dessutom kan det leda till överdrivna eller förvrängda slutsatser om samband och orsakssamband, vilket underminerar validiteten hos de erhållna resultaten. En forskare kan dras till felaktiga slutsatser eller underskatta effekterna av vissa prediktorer, vilket i sin tur kan påverka beslutsfattande och praktisk tillämpning av forskningsresultaten.
Vilka analyser påverkas?
Multikollinearitet påverkar främst analyser som involverar regressionsmodeller och försöker uppskatta parametrar för prediktorer. Bland dessa analyser är linjär regression särskilt mottaglig för problem som uppkommer på grund av hög korrelation mellan oberoende variabler. Andra modeller, som logistisk regression och koefficientvariation, är också känsliga för när flera prediktor är för starkt korrelerade.
Inom kvantitativ forskning är dessa analyser grundläggande för att förstå och predicera relationer mellan vari abler. När oberoende variabler är nära relaterade (hög korrelation), blir det, som tidigare nämnts, svårt för modellen att särskilja deras individuella effekter. Detta kan i sin tur leda till osäkra och förvrängda resultat. Det är avgörande att vara medveten om dessa känsligheter när man utformar och tolkar studier inom olika discipliner, inklusive samhällsvetenskap, psykologi och kognitionsvetenskap. I nästa avsnitt kommer vi att utforska hur man identifierar kollinearitet och dess konsekvenser.
Hur upptäcker man Multikollinearitet?
Att upptäcka multikollinearitet är avgörande för att förhindra felaktiga slutsatser och förvrängda resultat. Det finns flera metoder och tester tillgängliga för att identifiera detta fenomen:
- Korrelationsmatris: En grundläggande teknik är att undersöka korrelationsmatrisen för oberoende variabler.
- Variansinflationsfaktor (VIF): VIF mäter hur mycket varians i uppskattningen av en oberoende variabel ökar på grund av hög korrelation med andra variabler.
- Tolerans: Tolerans är det omvända av VIF och kan användas som ett komplementärt mått. Låga toleransvärden indikerar potentialla stora problem.
- Egenvektorer och egenvalues: Genom att beräkna egenvektorerna och egenvalues av korrelationsmatrisen kan man få insikt i vilka variabler som bidrar mest till multikollinearitet.
- Tillämpad visualisering: Använd scatterplots för att visuellt inspektera relationer mellan variabler och identifiera möjlig ulmtikollinearitet.
Att kombinera dessa metoder ger en mer holistisk förståelse och underlättar en noggrann upptäckt av problem med detta problem. Nästa steg efter identifiering är att överväga hur man hanterar detta fenomen, vilket kommer att utforskas senare i inlägget.
Tolkning av Resultaten (Korrelation, VIF, & Tolerans)
Att tolka resultaten från multikollinearitetstester är kritiskt för att fatta informerade beslut om huruvida man ska åtgärda problemet och hur man ska tolka de statistiska resultaten. Här är några viktiga aspekter:
- Korrelation över .8: En korrelation över .8 mellan två variabler anses ofta vara hög. Detta kan tyda på potentiell multikollinearitet, men det är ingen absolut regel. Det är viktigt att överväga sammanhanget och den specifika forskningsfrågan.
- VIF över 10: Ett VIF-värde över 10 indikerar hög multikollinearitet. Dock är det en grov riktlinje, och andra faktorer, som studiens natur och syfte, bör vägas in. Ibland tolereras högre VIF-värden beroende på kontext.
- Tolerans under .1: Låga toleransvärden, särskilt under .1, antyder hög multikollinearitet. Återigen är det viktigt att kontextualisera resultaten och överväga studiens mål.
Det är värt att notera att dessa cutoff-värden inte är absoluta sanningar utan riktlinjer. Att bedöma multikollinearitet innebär ofta en bredare bedömning, där man tar hänsyn till forskningens specifika kontext och mål. Resultaten bör alltid tolkas med hänsyn till den övergripande designen och syftet med studien för att fatta välgrundade beslut om hur man ska hantera problemen.
Multikollinearitetstester med Jamovi
För att utföra multikollinearitetstester i Jamovi, följ dessa steg:
- Öppna dataset i Jamovi: Starta Jamovi och öppna det dataset där du vill utföra analysen.
- Välj regression från Menyn: Gå till menyn och välj “Regression” för att öppna analysverktyget.
- Specificera prediktorer: Ange dina prediktorvariabler (Covariates) och beroende variabel i respektive fält.
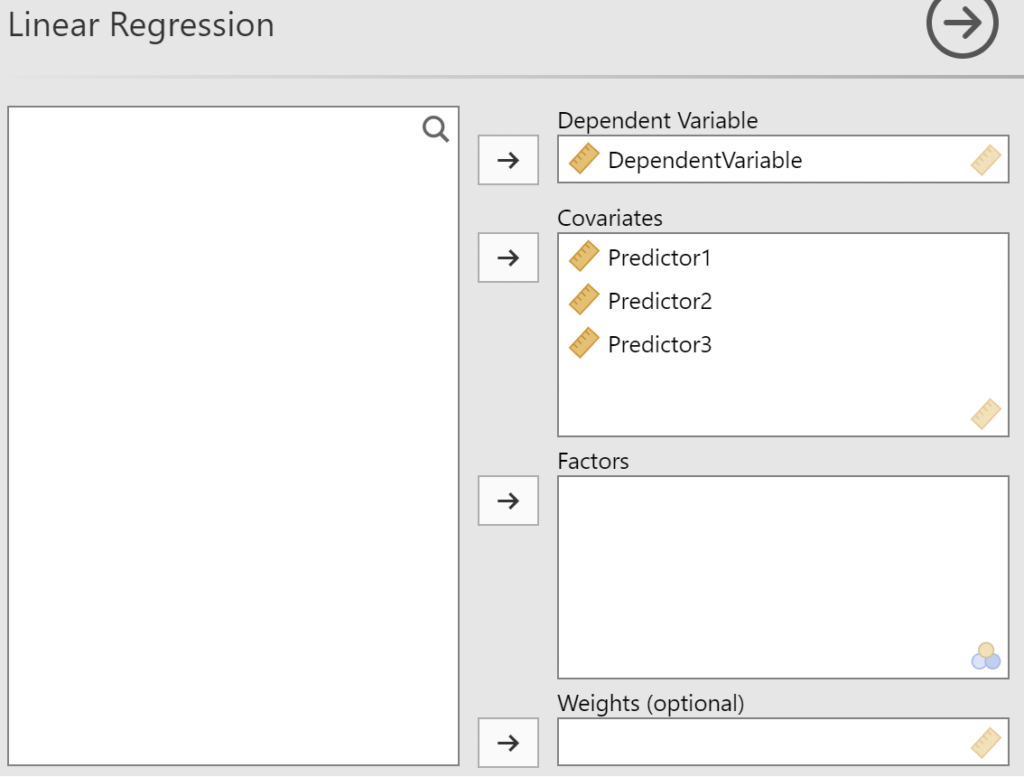
- Klicka på fliken “Assumptions Checks” och bocka för Collinearity statistics.
- Granska VIF-värden: I resultatfönstret, leta efter VIF-värden (Variance Inflation Factor) för varje prediktor. Höga värden över 10 kan indikera multikollinearitet.
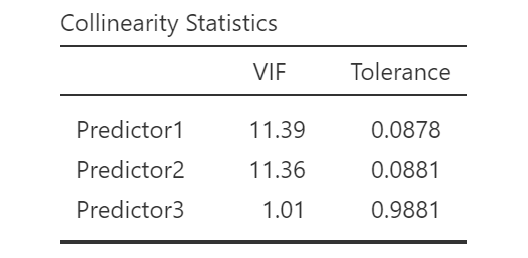
För att undersöka en korrelationsmatris i Jamovi efter att ha kört ovan tester, fortsätt med följande steg:
Undersök korrelationsmatrisen (frivilligt)
- I Jamovi, gå till menyn och välj “Regression”, igen
- Klicka på “Correlation Matrix.”
- Välj dina prediktorer.
- Granska korrelationskoefficienter:
- Studera korrelationsmatrisen för att identifiera höga korrelationskoefficienter mellan dina prediktorer
- Tolka resultaten:
- Integrera informationen från korrelationsmatrisen med exempelvis VIF-värdena för en mer holistisk bedömning.
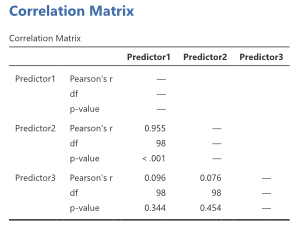
Att undersöka korrelationsmatrisen kompletterar testerna och ger en djupare förståelse för sambanden mellan variablerna, vilket är avgörande för att göra välgrundade slutsatser i kvantitativ analys. Kom ihåg att anpassa din tolkning baserat på kontexten för din studie.
Testning med R
För att utföra multikollinearitetstester i R, kan du använda paket som “car” för att beräkna VIF och tolerans. Använd funktionerna vif() och corr() för att erhålla relevanta värden. Vi kommer gå igenom, steg-för-steg, för alla de olika testerna i de följande delarna.
För att beräkna VIF i R och visualisera resultaten, följ dessa steg:
1. Ladda Nödvändiga Paket
library(car)2. Läs in ditt data
df_reg <- read.csv("data.csv")Code language: CSS (css)3. Skapa din regressionsmodell:
fit <- lm(BeroendeVariabel ~ Prediktor1 +
Prediktor2 +
Prediktor3, data = df_reg)Code language: HTML, XML (xml)I koden ovan skapar vi en regressionsmodell genom att använda funktionen lm (linear model) i R. Vi specificerar modellen genom att ange den beroende variabeln (BeroendeVariabel) och dess samband med flera oberoende variabler (Prediktor1, Prediktor2, Prediktor3)
4. Beräkna VIF:
vif_results <- vif(fit)I koden ovan får vi VIF-värden för våra tre prediktorer.
5. Visa resultaten med hjälp av print():
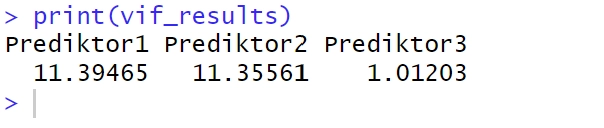
6. Visualisera VIF med ett stapeldiagram
Med hjäp av R och ggplot2 kan vi även visualisera VIF :
# Anta att vif_results är en vektor med VIF-resultaten
vif_results <- vif(fit)
# Skapa en dataframe för ggplot2
vif_data <- data.frame(Prediktor = colnames(X), VIF = vif_results)
# Skapa ggplot2-plot
library(ggplot2)
ggplot(vif_data, aes(x = Prediktor, y = VIF)) +
geom_bar(stat = "identity", fill = "skyblue", color = "black") +
labs(title = "VIF Resultat",
x = "Prediktor",
y = "VIF") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1),
axis.title.x = element_blank())
Code language: PHP (php)
I koden ovan skapar vi visuella representationer av Variance Inflation Factor (VIF) med hjälp av ggplot2 i R. Först extraherar vi kolumnnamnen för de prediktorer som är av intresse och skapar sedan en dataframe som kombinerar dessa namn med de beräknade VIF-resultaten. Därefter använder vi ggplot2 för att generera ett stapeldiagram där varje stapel representerar en prediktor och dess associerade VIF-värde.
För att beräkna Tolerans i R följ dessa steg:
Tolerans är enkelt att beräkna i R:
1. Ladda Nödvändiga Paket
library(car)2. Läs in ditt Data
df_reg <- read.csv("data.csv")Code language: R (r)3. Skapa din Regressionsmodell
fit <- lm(BeroendeVariabel ~ Prediktor1 +
Prediktor2 +
Prediktor3, data = df_reg)Code language: HTML, XML (xml)I den givna kodblocket formar vi en regressionsmodell med hjälp av funktionen lm (linear model) i R. Vi definierar modellen genom att ange den responsvariabeln (BeroendeVariabel) och dess relation till ett antal oberoende variabler (Prediktor1, Prediktor2, Prediktor3).
4. Beräkna Tolerans
fit <- lm(BeroendeVariabel ~ Prediktor1 +
Prediktor2 +
Prediktor3, data = df_reg)Code language: R (r)I koden ovan får vi Tolerans-värden för våra tre prediktorer genom att dela 1 genom VIF-värdena.
Genom att följa dessa steg får du en översikt över variablernas toleransnivåer och kan bedöma eventuella problem i din regressionsanalys.
Skapa en korrelationsmatris i R
För att skapa en korrelationsmatris kan du följa följande steg:
1. Läs in Ditt Data
df_reg <- read.csv("data.csv")Code language: CSS (css)I kodblocket ovan läser vi in vår data med read.csv (precis som i tidigare exampel).
2. Skapa Korrelationsmatrisen
cor_mat <- cor(df_reg[,c("Prediktor1",
"Prediktor2",
"Prediktor3" )])Code language: JavaScript (javascript)
I kodblocket ovan skapas vår korrelationsmatris med -funktionen. Vi använder vår dataframe, df_reg, och väljer specifika prediktorer, nämligen “Prediktor1,” “Prediktor2,” och “Prediktor3,” med hjälp av c(). Sedan lagras den resulterande korrelationsmatrisen i variabeln cor_mat.
3. Visa Resultaten
print(cor_mat)Code language: PHP (php)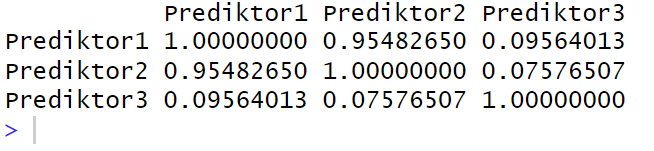
Genom att följa dessa steg kan du utforska korrelationerna mellan variabler och identifiera möjliga problem i din dataset.
Vad Gör om Vi har Upptäckt Multikollinearitet ?
Om Multikollinearitet upptäcks efter analyser av resultatet, finns det flera åtgärder för att hantera detta fenomen. En strategi är att eliminera en eller flera prediktorer som uppvisar hög korrelation, vilket kan minska effekterna. En annan metod är att kombinera högt korrelerade variabler och skapa en ny, sammanfogad variabel, vilket kan minska den överdrivna effekten av korrelation (ett så kallat kompositmått). Att öka stickprovsstorleken kan också vara en åtgärd för att minska problemet med att flertalet variabler korrelerar för starkt.
Utvärdera även möjligheten att använda andra metoder som ridge regression eller principal component regression, vilka är konstruerade för att hantera multikollinearitet. Slutligen är det viktigt att överväga den praktiska betydelsen högt korrelerande prediktorer i förhållande till studiens övergripande syfte och om den faktiskt påverkar den vetenskapliga tolkningen av resultaten. Att vara medveten om multikollinearitet och vidta lämpliga åtgärder för att mildra dess effekter är avgörande för att säkerställa att resultaten från statistiska analyser är tillförlitliga och trovärdiga. Det är också rekommenderat att samråda med experter inom området för att få insikt och vägledning om hur man bäst hanterar specifika utmaningar som kan uppstå till följd av korrelerade prediktorer.
När du diagnosticerat din regressionsmodell och fattat beslut hur du ska hantera eventuell problem kan du även göra dena deskriptiva analyser med Jamovi eller R.
Sammanfattning
Sammanfattningsvis belyser detta inlägg viktiga aspekter av multikollinearitet inom statistiska analyser. Vi har diskuterat dess definition, påverkan på olika analyser, och hur man upptäcker och åtgärdar det. Att hantera korrelerade variabler är avgörande för att säkerställa trovärdiga resultat från våra regressionsanalyser och de tolkningar vi kan göra från resultaten i forskning. Om du finner denna information användbar för din uppsats, rapport eller artikel, var vänligen referera till den (se nedan för en färdig APA 7-referens). Dela gärna detta inlägg på sociala medier och lämna eventuella frågor eller kommentarer nedan för ytterligare diskussion.
Resurser
Här är ett par fler statistik- och metodrelaterade inlägg som kan vara till hjälp:
- Validitet och Reliabilitet i Kognitionsvetenskap: Teori och Exempel
- Korrelationsanalys: Korrelationskoefficient i R eller Excel
- Korstabell: Vad är det & Hur Man Gör en Med Excel & SPSS
