Mann Whitney U Test in R: A Comprehensive Guide

Mann Whitney U test in R is a useful tool for comparing two independent samples when the parametric assumptions of the t-test are not met. For example, we might use it to compare the performance of two groups of participants on a cognitive task that produces ordinal or skewed data. In this post, we will explain how to perform and interpret the Mann Whitney U test in R and show some examples of its application in cognitive psychology. To perform the Mann Whitney U test we can use the `wilcoxon

Outline

Prerequisites
What is Mann Whitney U Test in R?
How to do Mann Whitney U Test in R

Interpreting the Mann Whitney U Test
Packages to use to do Mann Whitney U Test
Conclusion

Resources

Outline

The structure of the post is as follows. First, we introduce the Mann Whitney U test, highlighting its significance in statistical analysis. Next, we learn how to execute the test in R, demonstrating its implementation with a simple example. Following this, we quickly look at how to interpret the results of the test. Additionally, we discuss the packages available in R for conducting the Mann Whitney U test. In this post, you will gain a thorough understanding of the Mann Whitney U test and its application in R. The post will hopefully empower you to make informed decisions in your data analysis endeavors.

Prerequisites

Before learning the practices of the Mann Whitney U test in R, it is essential to have a basic understanding of R programming and data manipulation. Familiarity with reading and handling your own data in R is a must. Additionally, knowledge of how to install R packages is necessary if you intend to use suggested packages. With these prerequisites in place, you will be well-equipped to explore the intricacies of the test and apply it to your own data with confidence.

What is Mann Whitney U Test in R?

Mann Whitney U test in R is a statistical procedure that allows you to compare the distributions of two independent samples. We can use it to test whether they are significantly different. The test is also known as the Wilcoxon rank sum test or the Mann-Whitney-Wilcoxon test. It is a nonparametric alternative to the t-test, which assumes that the samples are normally distributed and have equal variances. The Mann Whitney U test does not make these assumptions. Therefore, we can use it when the data are ordinal, skewed, or have outliers.

The Mann Whitney U test ranks the combined data from both samples. Furthermore, the sum of ranks for each sample. The test statistic, U, is the smaller of the two sums of ranks. The smaller U is, the more evidence there is that the samples come from different populations. The test also provides a p-value, which is the probability of obtaining a result as extreme or more extreme than the observed one, under the null hypothesis that the samples are from the same population. A small p-value (usually less than 0.05) indicates that the null hypothesis can be rejected and that there is a significant difference between the samples.

How to do Mann Whitney U Test in R

To perform the Mann Whitney U test in R, you need to have two vectors of data that represent the two independent samples. For example, suppose you have a vector x that contains the scores of 10 students on a math test and a vector y that contains the scores of 12 students on the same test but from a different class. You want to test whether the two classes have different math achievement levels. You can use the following code to do the Mann Whitney U test in R:

# Generate example data
x <- c(85, 88, 85, 76, 90, 76, 81, 74, 91, 78)
y <- c(62, 69, 65, 73, 79, 77, 73, 82, 70, 67, 81, 76)

# Perform the Mann Whitney U test
wilcox.test(x, y)Code language: R (r)

Interpreting the Mann Whitney U Test

The output shows that the test statistic, W, is 101.5 and the p-value is 0.006752. Since the p-value is smaller than 0.05, we reject the null hypothesis that the two samples come from the same population. Therefore, we conclude that there is a significant difference between the two classes’ math scores.

Packages to use to do Mann Whitney U Test

The base R function wilcox.test() can perform the Mann Whitney U test for two independent samples, as shown in the previous example. However, some packages provide more options and features for doing the test. Here are some of them:

rstatix: This package provides a collection of functions and datasets that are useful for various aspects of data analysis. The function mannWhitney() in this package can perform the Mann Whitney U test and also calculate the effect size, confidence interval, and power of the test. It can also plot the distributions of the samples and the ranks.

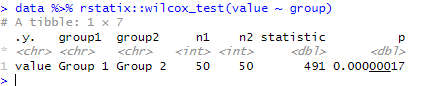
Mann Whitney U test with the rstatix package.

ggstatsplot: This package combines the functionalities of ggplot2 and various statistical tests to create plots with statistical details. The function ggbetweenstats() in this package can create a boxplot or a violin plot of the two samples and add the results of the Mann Whitney U test, along with the effect size and the confidence interval. It can also handle grouped data and multiple comparisons.

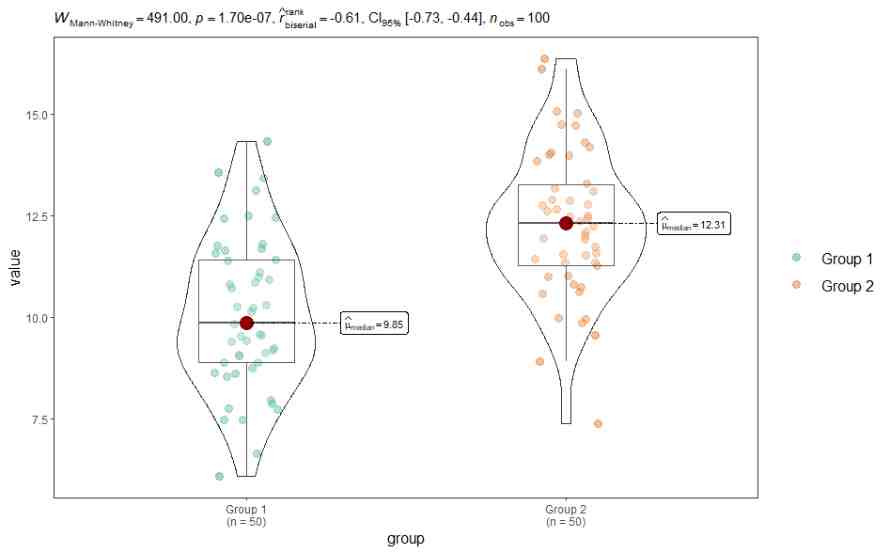
mann whitney u test in r on a plot — ggstatsplot figure

Conclusion

Mann Whitney U test in R is useful for comparing the distributions of two independent samples and testing whether they are significantly different. The test is a nonparametric alternative to the t-test. Moreover, we can use it when the data are ordinal, skewed, or have outliers. The base R function wilcox.test() can perform the test. However, some packages provide more options and features for doing the test, such as rstatix, and ggstatsplot. In this guide, we have explained the test, how to do it, and what packages to use in R. Please leave a comment below to show your appreciation and suggestions or request any topics that you want to have covered on the blog. Oh, and do not forget to share the post on your social media accounts and refer to it if you found it helpful.

Resources

Here are some more data analysis related blog post you may find helpful:

Master MANOVA in R: One-Way, Two-Way, & Interpretation