Korrelationsanalys är en statistisk metod som mäter hur två eller flera variabler är relaterade till varandra. Det kan hjälpa oss förstå mönster, trender och samband i vårdata och svara på frågor som:
- Hur påverkar arbetsminneskapacitet läsförståelsen?
- Hur varierar användarnöjdhet med webbplatsens användbarhet?
- Hur påverkar humöret beslutsfattandet?
Korrelationsanalys är relativt enkelt att utföra, men det gäller förstås att ha koll på en del saker. Till exempel, riktningen på sambandet kan vara positivt eller negativt. Vidare finns det olika typer av korrelationskoefficienter, var och en med sina egna antaganden, begränsningar och tolkningar. Att välja fel typ av korrelation kan leda till vilseledande eller felaktiga resultat. I denna bloggpost kommer vi att förklara grunderna i korrelationsanalys, de olika typerna av korrelationer vi kan utföra och hur man utför korelationtest i R och i Excel, två populära program och en gratis programvara för dataanalys (R). Vi kommer även kika på hur man tolkar sina resultat, när man väl har fått dem. Det vill säga, vi kommer även behandla vad korrelation faktiskt betyder (och inte betyder).
Innehållsförteckning
- Olika Typer av Korrelationsanalyser
- Hur man utför Korrelationsanalys i R
- Korrelationsanalys i Excel
- Sammanfattning
- Andra Källor
- Referera till Bloggposten
- Resurser
Olika Typer av Korrelationsanalyser
Innan vi utför en korrelationsanalys behöver vi veta vilken typ av korrelationskoefficient vi kan använda. Korrelationskoefficienten är ett numeriskt värde som varierar från -1 till 1 och indikerar styrkan och riktningen av förhållandet mellan dina variabler. En positiv korrelation innebär att variablerna tenderar att öka eller minska tillsammans, medan en negativ korrelation innebär att de tenderar att röra sig i motsatta riktningar. En korrelation nära 0 innebär att det inte finns något linjärt förhållande mellan variablerna.
Dock är inte alla korrelationskoefficienter detsamma. Beroende på datas natur och distribution kan vi behöva använda olika typer av korrelation, såsom:
Pearsons Korrelationskoefficient
Pearson-korrelationen är den vanligaste typen av korrelation och mäter det linjära förhållandet mellan två kontinuerliga variabler som är normalt fördelade. Vi kan till exempel använda Pearson-korrelation för att mäta förhållandet mellan arbetsminneskapacitet och läsförståelse, Alternativt, kan vi använda det för att mäta relationen mellan webbplatsens användbarhet och användarnöjdhet.
För att använda Pearson-korrelation måste vi kontrollera följande antaganden:
- Variablerna är kontinuerliga och har ett linjärt förhållande.
- Variablerna är normalt fördelade, eller åtminstone ungefär så.
- Variablerna har inga utstickare, eller åtminstone minimala.
- Variablerna har homoskedasticitet, vilket innebär att variansen för en variabel är liknande över värdena för den andra variabeln.
Tolkning:
Om dessa antaganden är uppfyllda kan vi tolka Pearson-korrelationskoefficienten på följande sätt:
- En positiv korrelation innebär att variablerna tenderar att öka eller minska tillsammans, och ju närmare koefficienten är 1, desto starkare är förhållandet.
- En korrelation nära 0 innebär att det inte finns något linjärt förhållande mellan variablerna, eller att förhållandet är mycket svagt.
- En negativ korrelation innebär att variablerna tenderar att röra sig åt motsatta håll, och ju närmare koefficienten är -1, desto starkare är förhållandet.
Vi kan också testa den statistiska signifikansen för Pearson’s korrelationskoefficient, vilket säger oss att korrelationen troligen beror på slumpen eller inte. En p-värde mindre än .05 innebär att korrelationen är signifikant, och inte beror på slumpen.
Spearman Korrelationskoefficient
Spearman-korrelation är en icke-parametrisk typ av korrelation och mäter det monotoniska förhållandet mellan två variabler som är ordinala eller har sned fördelning. Ett monotoniskt förhållande innebär att variablerna tenderar att förändras i samma riktning, men inte nödvändigtvis med en konstant hastighet.
Vi kan använda Spearman-korrelation för att mäta förhållandet mellan, exempelvis, humör och beslutsfattande, eller mellan utbildningsnivå och inkomst.
För att använda Spearman-korrelation måste vi kontrollera följande antaganden:
- Variablerna är ordnade, eller kan omvandlas till ordnade, vilket innebär att de har en meningsfull ordning.
- Variablerna har ett monotoniskt förhållande, vilket innebär att de inte ändrar riktning mer än en gång.
Tolkning
Som med Pearson’s korrelationsanalys så tolkar viSpearmans så att:
- En positiv korrelation innebär att variablerna tenderar att öka eller minska tillsammans, och ju närmare koefficienten är 1, desto starkare är förhållandet.
- En negativ korrelation innebär att variablerna tenderar att röra sig åt motsatta håll, och ju närmare koefficienten är -1, desto starkare är förhållandet.
- En korrelation nära 0 innebär att det inte finns något monotoniskt förhållande mellan variablerna, eller att förhållandet är mycket svagt.
Återigen, kan vi också testa den statistiska signifikansen för Spearman-korrelationskoefficienten. Ett p-värde mindre än 0,05 innebär att korrelationen är signifikant, och inte beror på slumpen.
Kendall Korrelationskoefficient
Kendall-korrelation är en annan icke-parametrisk typ av korrelation och mäter den ordinala associationen mellan två variabler som är ordinala eller har lika rankning. Det är liknande Spearman-korrelation, men det är baserat på antalet konsekventa och inkonsekventa par av observationer, snarare än skillnaden i rangordning. Vi kan till exempel använda Kendall-korrelation för att mäta sambandet mellan användarupplevelse och kognitiv belastning, eller mellan perception och beslutsfattande.
För att använda Kendall-korrelation måste vi kontrollera följande antaganden:
- Variablerna är på ordinalskala, eller kan omvandlas till ordinaskalal.
- Variablerna har ett stort antal distinkta värden, eller ett litet antal kopplingar, vilket gör att det inte finns många observationer med samma rang.
Tolkning
Tolkningen av Kendalls korrelation är liknande Pearson och Spearmans:
- En positiv korrelation innebär att variablerna tenderar att öka eller minska tillsammans, och ju närmare koefficienten är 1, desto starkare är sambandet.
- En negativ korrelation innebär att variablerna tenderar att röra sig i motsatta riktningar, och ju närmare koefficienten är -1, desto starkare är sambandet.
- En korrelation nära 0 betyder att det inte finns någon ordinalassociation mellan variablerna, eller att associationen är mycket svag.
Precid som med de övriga två korrelationskoefficienternas så kan vi också testa den statistiska signifikansen för Kendalls korrelationskoefficient.
Hur man utför Korrelationsanalys i R
Vi kan använda R för att utföra korrelationsanalys med olika typer av korrelationskoefficienter och för att skapa vackra och informativa plotter för att visa dina resultat. I det här avsnittet kommer vi att visa dig hur vi gör det i R med några exempel.
För att utföra korrelationsanalys i R måste vi använda basfunktionen cor(). Denna funktion två argument: x och y, som är vektorerna eller matriserna för variabler vi vill korrelera. Här kan vi också ange vilken typ av korrelationskoefficient vi vill använda med metodargumentet, vilket kan vara något av följande: “pearson”, “spearman” eller “kendall”. Som standard använder funktionen cor() Pearson-korrelation. För att även testa signifikansen behöver vi emellertid använda cor.test().
Pearson’s Korrelationsanalys
För att beräkna sambandet mellan uppmärksamhetsnivå (attention) och reaktionstid (reactiontime) kan vi göra som följer:
pearson_corr_interval <- cor(data$attention,
data$reactiontime,
method = "pearson")Code language: R (r)Genom att använda cor() som i kodsnutten ovan får vi alltså fram sambandet mellan våra två variabler (attention och reactiontime).

Vi ser att det finns ett (väldigt) litet negativt samband mellan uppmärksamhetsnivå och reaktionstid. Om vi istället använder cor.test() kan vi testa om sambandet är stastiskt signifikant:
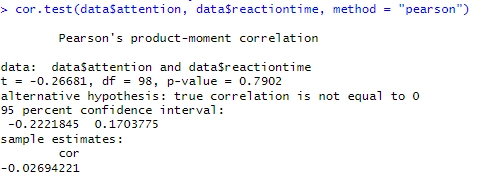
cor.test(data$attention, data$reactiontime, method = "pearson")Code language: R (r)Resultaten visar att korrelationskoefficienten är -0.0269 (något vi redan visste, förstås). Som tidigare nämn indikerar det en väldigt svag eller försumbar negativ korrelation mellan de två uppmärksamhetsnivå och reaktionstid. Vidare är p-värdet 0.7902, vilket är över alfa (0,05) och indikerar att korrelationen inte är statistiskt signifikant. Det finns inte tillräckligt med bevis för att förkasta nollhypotesen om att korrelationen är lika med noll. Det 95-procentiga konfidensintervallet sträcker sig från -0.222 till 0.170, vilket stöder att korrelationen är nära noll.
I nästa del kommer vi kolla på hur vi utför Spearmans korrelationsanalys i R.
Spearmans Rangkorrelation
För att utföra Spearmans rangkorrelation så använder vi återigen cor() och cor.test():
spearman_corr <- cor(data$attention,
data$problemsolving,
method = "spearman")Code language: PHP (php)I detta exempel kan vi se att vi har en positiv stark korrelation (0,73), men är den statistiskt signifikant? Det är nästa steg:
cor.test(data$attention, data$problemsolving,
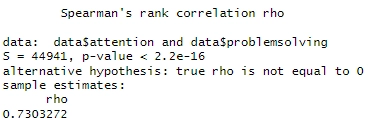
method = "spearman")Code language: R (r)Vi kan se från outputen att resultaten visar en Spearman-rankkorrelation mellan uppmärksamhet och problemlösning. Rho-koefficienten är 0.7303, vilket indikerar en stark positiv korrelation mellan de två variablerna, som tidigare nämnt. Slutligen kan vi se att p-värdet är under alfa (0,05). Därmed kan vi förkasta nollhypotesen om att korrelationen är lika med noll. Detta stöder att det finns ett samband mellan uppmärksamhet och problemlösning.
Kendalls Rangordnings-Koefficient
Vi kan förstås återigen använda både cor() och cor.test(), som i exemplen ovan, för att göra denna typ av korrelationsanalys:
kendall_corr <- cor(data$cognitive_load,
data$perceived_stress, method = "kendall")
kendall_corr
cor.test(data$cognitive_load,
data$perceived_stress, method = "kendall")Code language: PHP (php)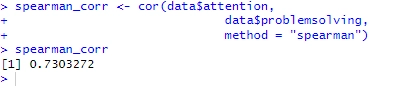
Givetvis får vi ett resultat, som inkluderar p-värdet, när vi använder cor.test() och method = "kendall"också.
En av fördelarna med att använda R för korrelationsanalys är att vi enkelt kan skapa diagram för att visualisera våra resultat. Till exempel kan vi använda paketet ggplot2 för att skapa spridningsdiagram med regressionslinjer och konfidensintervall för varje par av variabler, och för att lägga till korrelationskoefficienter och p-värden till vår figur. Vi kan också använda funktionen ggpairs() från paketet GGally för att skapa en matris av spridningsdiagram för alla variabler i din dataframe, och för att visa korrelationskoefficienter och p-värden i de övre eller nedre trianglarna. Till exempel kan vi använda följande kod för att skapa en plottmatris för dataramen df:
library(GGally)
ggpairs(df, upper = list(continuous = wrap("cor", size = 3, method = "pearson")),
lower = list(continuous = wrap("points", alpha = 0.5)))Code language: PHP (php)Som vi kan se visar plottmatrisen spridningsdiagrammen för varje variabelpar i den nedre triangeln, och Pearsons korrelationskoefficienter och p-värden i den övre triangeln. Vi kan också ändra argumentet “method” till “spearman” eller “kendall” för att använda olika typer av korrelationskoefficienter. I nästa del ska vi kika på hur man utför korrelationsanalys i Excel.
Korrelationsanalys i Excel
Jämfört med R så är det förstås lite mer begränsat när det kommer till korrelationsanalyser i Excel. Här är emellertid de steg vi kan utföra för att beräkna en korrelationskoefficient i Excel:
1. Öppna din Data
Första steget är att starta Excel och ladda in din data.
2. Välj Formler och Infoga en Funktion
Det nästa steget är att klicka på “Formler”-fliken för att sedan välja “Infoga en Funktion”.
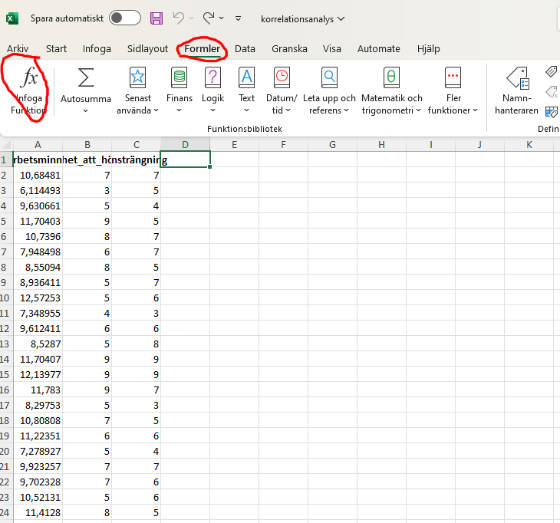
3. Sök/Välj korrel-funktionen
Tredje steget innebär att välja korrel funktionen.
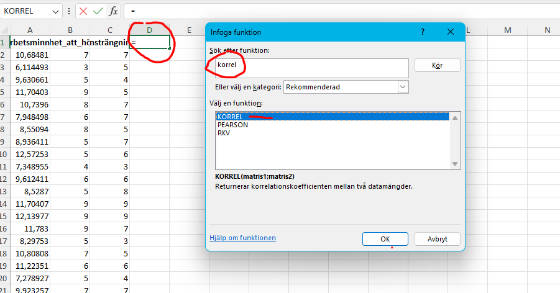
4. Välj Variabler att Korrelera
Här ska vi bara välja de kolumner (dvs. våra två variabler) som vi vill beräkna korrelationskoefficienten för.
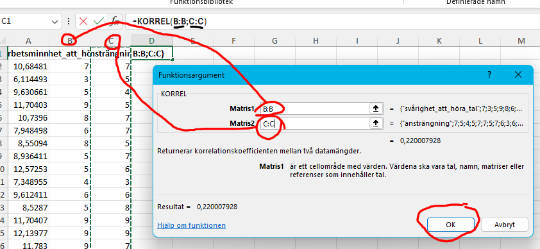
5. Utför Korrelationsanalys
Slutligen kan vi beräkna korrelationskoefficienten. Detta gör vi genom att trycka “OK” (se bild ovan). Vi får våra resultat i den nya cellen vi markerade:
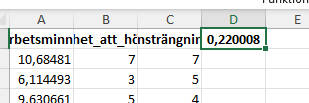
Det vi kan se är att vi har en svag korrelation mellan svårighet att höra och ansträngning.
Sammanfattning
Korrelationsanalys är en användbar och väl använd teknik för att utforska relationerna mellan variabler i vår data. Vi måste dock vara försiktiga och välja rätt typ av korrelationskoefficient som passar vår data och forskningsfråga. I den här bloggposten har gått igenom grunderna i korrelationsanalys, de olika typerna av korrelation vi kan utföra, och hur vi gör det i R och i Excel, två populära programvaruverktyg.
Andra Källor
Referera till Bloggposten
Jag ser gärna att du refererar till denna bloggpost om den var till nytta. Använd denna om du vill följa APA 7:
Marsja, E. (2024, April 9). Korrelationsanalys: Korrelationskoefficient i R eller Excel. https://www.marsja.se/korrelationsanalys-korrelationskoefficient-i-r-eller-excel/
Resurser
Här är lite fler resurser som kan vara hjälpsamma.
- Deskriptiva Analyser: Exempel med Jamovi och R Statistik
- Validitet och Reliabilitet i Kognitionsvetenskap: Teori och Exempel
- Psykometri i Kognitionsvetenskapen: Exempel & Egenskaper
- Korstabell: Vad är det & Hur Man Gör en Med Excel & SPSS
